In this case, we have an isosceles triangle, in this kind of figures the height (segment that goes from the vertex E to the base) bisects the upper angle, then the angle
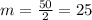
Then, the measure of the upper angle of the triangle formed to the left equals 25°, the height of the triangle forms a right angle with the base of the triangle, then the measure of the angle on the right (next to y°) equals 90°. The sum of the internal angles of a triangle always equals 180°, then we can formulate the following expression:
x° + 25° + 90° = 180°
x° + 115° = 180°
x° + 115° - 115° = 180° - 115°
x° = 65°
Then x° equals 65°
As mentioned, the height forms a right angle with the base of the triangle, then the measure of the angle y° equals 90°
The length of the side LN equals twice the length of the base of the left triangle, then we get:
LN = 2*7 = 14
Then, the length of LN equals 14 cm