We are asked to find the area of the shaded region.
Notice that the overall figure is a rectangle and the missing area is a triangle.
The area of the rectangle is given by

Where w is the width and l is the length of the rectangle.
width = 7 m
length = 16 m
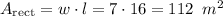
So, the area of the rectangle is 112 m²
The area of the triangle is given by
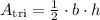
Where b is the base and h is the height of the triangle.
base = 7 m
height = 8 m
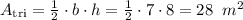
So, the area of the triangle is 28 m²
The area of the shaded region can be found by subtracting the area of the triangle from the area of the rectangle.
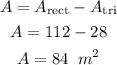
Therefore, the area of the shaded region is 84 m²