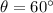Question

The regulation height of a basketball hoop is 10 feet. Let the location of thebasket be represented in the coordinate plane by the point (0, 10). Let the ballbe thrown at a 45° angle with the ground.1. Suppose Nancy is standing a horizontal distance of 10 feet from thebasket at the point (-10, 0), and she shoots a basket from 6 feet in theair with an initial velocity of 22 ft/s.Question 1)C. Will Nancy make the basket? Defend your reasoning.D. Use appropriate tools strategically. Experiment on yourcalculator with different direction angles until the player makes abasket. What angle did you use?

Answer 1

(A): Using the equations of motion, we can determine the answer as follows:

`\begin{gathered} x(t)=x_(\circ)+v_(\circ)cos(\theta)t\rightarrow(1) \\ \\ y(t)=y_(\circ)+v_(\circ)sin(\theta)-(1)/(2)gt^2\rightarrow(2) \\ \\ y(x)=xtan(\theta)-(g)/(2(v_(\circ))^2cos^2(\theta))x^2\rightarrow(3) \end{gathered}`

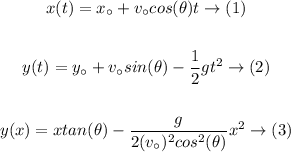
formula (3) is obtained from (1) and (2), using equation (3) the answer is determined as below:

`\begin{gathered} y(x)=xtan(\theta)-(g)/(2(v_(\circ))^2cos^2(\theta))x^2 \\ \\ v_(\circ)=22\text{ f/s} \\ \\ \theta=45 \\ \\ g=32.1522\text{ f/s} \\ \\ y(x)=xtan(45)-(32.1522)/(2*22^2cos^2(45))x^2 \\ \\ y(x)=x-(32.1522)/(2*22^2cos^2(45))x^2 \\ \\ y(x)=x-(32.152,2)/(484)x^2 \\ \\ y(x)=x-0.06643x^2 \\ \\ (x,y)\rightarrow\text{ Adjusting the position for the shift gives:} \\ \\ y(x)=[(x+10)-0.06643(x+10)^2]+6\rightarrow(4) \end{gathered}`

The plot of the (4) reveals the following:

Therefore the answer is no.

(D) Trying a new angle theta = 60 degrees gives the following new answer:

Therefore the answer is:

`\theta=60^(\circ)`