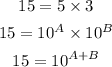Question

Logarithm 6) If log 5 = A and log 3 = B, find the following in terms of A and B:

Answer 1

Explanations:

Given the following parameters:

log 5 = A

log 3 = B

According to the law of product and quotient of logarithm as shown:

`\begin{gathered} \log AB=\log A+\log B \\ \log ((A)/(B))=\log A-\log B \\ \log A^b=b\log A \end{gathered}`

Applying the laws of logarithm in solving the given logarithm

`\begin{gathered} a)\log 15 \\ =\log (5*3) \\ =\log 5+\log 3 \\ =A+B \end{gathered}`

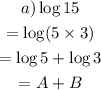
For the expression log(25/3)

`\begin{gathered} b)\log ((25)/(3)) \\ =\log ((5^2)/(3)) \\ =\log 5^2-\log 3 \\ =2\log 5-\log 3 \\ =2A-B \end{gathered}`

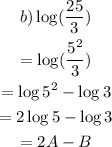
For the expression log135

`\begin{gathered} \log (135) \\ =\log (5*27) \\ =\log (5^{}*3^3) \\ =\log 5^{}+\log 3^3 \\ =\log 5+3\log 3 \\ =A+3B \end{gathered}`

For the expression log₅27

`\begin{gathered} \log _527 \\ =(\log 27)/(\log 5) \\ =(\log 3^3)/(\log 5) \\ =(3\log 3)/(\log 5) \\ =(3B)/(A) \end{gathered}`

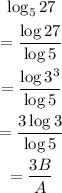
For the expression log₉625

`\begin{gathered} \log _9625 \\ =(\log 625)/(\log 9) \\ =(\log 5^4)/(\log 3^2) \\ =(4\log 5)/(2\log 3) \\ =\frac{\cancel{4}^2A}{\cancel{2}B} \\ =(2A)/(B) \end{gathered}`

For the value of 15, this can be expressed as shown. Since:

`\begin{gathered} \log 5=A;10^A=5 \\ \log 3=B;10^B=3^{} \end{gathered}`

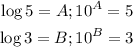
Since 15 = 5 × 3, writing it in terms of A and B will be expressed as:

`\begin{gathered} 15=5*3 \\ 15=10^A*10^B \\ 15=10^(A+B) \end{gathered}`