i)
The vertex form of a quadratic equation of a parabola opening upwards or downwards is,
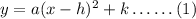
Here, (h,k) is the coordinates of the vertex of the parabola. If a is positive, the parabola is facing up and if a is negative, the parabola is facing down.
The given equation of parabola is,
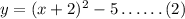
So, the given equation is in the vertex form of the quadratic equation.
Comparing equations (1) and (2), we get
a=1, h=-2, k=-5.
Since a is positive, the parabola opens upwards. The coordinates of the vertex of the parabola is (-2,-5).