Question

The probability that an employee will be late to work at a large corporation is 0.21. What is the probability on a given day that in a department of 5 employees at least 3 are late ?

Answer 1

Given:

Number of employees are 5.

Probability that an employee will be late to work at a large corporation is 0.21.

The given data follows binomial distribution,

`\begin{gathered} X\text{ \textasciitilde{}B(n,p,q)} \\ n=5 \\ p=0.21 \\ q=1-p=1-0.21=0.79 \\ P(X=x)=^nC_xp^xq^(n-x) \end{gathered}`

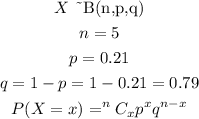
The probability that at least 3 employees are late is given as,

`\begin{gathered} P(X\ge3)=P(X=3)+P(X=4_{})+P(X=5) \\ P(X\ge3)=^5C_3(0.21)^3(0.79)^(5-3)+^5C_4(0.21)^4(0.79)^(5-4)+^5C_5(0.21)^5(0.79)^(5-5) \\ P(X\ge3)=0.0578+0.0077+0.0004 \\ P(X\ge3)=0.0659 \end{gathered}`

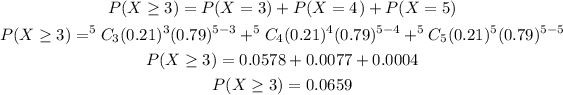
Answer: The probability that in a department of 5 employees at least 3 are late is 0.0659.