Question

Hello! Please check the image attached to see the question!

Answer 1

To solve this question, we must break down the question into different scenarios.

The speed expression for the first rider is:

`\begin{gathered} s=(d)/(t) \\ \text{let us make the distance the first rider covers as y.} \\ d=y\text{ miles} \\ t=3\text{ hours.} \\ s_1=(y)/(3) \end{gathered}`

The speed expression for the second cyclist:

`\begin{gathered} s=(d)/(t) \\ the\text{ first rider covered a distance of y miles, the remaining distance } \\ \text{left for the second cyclist to cover is:} \\ (108-y)\text{miles at the same time of 3 hours.} \\ s_2=(108-y)/(3) \end{gathered}`

Since one cyclist cycles 3 times as fast as the other:

It is expressed thus:

`\begin{gathered} s_1=3* s_2 \\ s_1=3s_2 \end{gathered}`

Now substitute the values for the speed expression into the expression above, we will have:

`(y)/(3)=3*((108-y)/(3))`

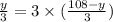
By solving the above expression, we will get the value of y (part of the distance travelled) and we can get the speed of the faster cyclist.

`\begin{gathered} (y)/(3)=(324-3y)/(3) \\ y=324-3y \\ y+3y=324 \\ \end{gathered}`
`\begin{gathered} 4y=324 \\ y=(324)/(4) \\ y=81\text{ miles.} \\ \\ So\text{ the speed of the faster cyclist will be:} \\ _{}=(y)/(3) \\ =\frac{81\text{ miles}}{3\text{ hours}} \\ =27mi\text{/h} \end{gathered}`

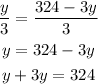
The speed of the faster cyclist is 27 mi/h.