Question

A girl ties a rope securely to the windowsill of a tower and climbs down to the base of it. She is with a group of friends and wants them to come down too, but easier. She ties the other end of the rope to a tree 30m down and 60m away horizontally, creating a zipline. The first person down the zip line weighs 80 kg. How quickly does he accelerate, and how long does it take for him to reach the end of the zipline?

Answer 1

Acceleration = 4.38 m/s²

Time = 5.54 s

Step-by-step explanation:

We can represent the situation as follows:

So, first, we need to find the angle θ. Using trigonometric functions, we get:

`\begin{gathered} \tan \theta=(opposite)/(adjacent) \\ \text{tan}\theta=(60)/(20) \\ \tan \theta=2 \\ \theta=tan^(-1)(2)=63.43 \end{gathered}`

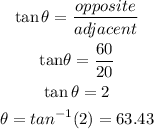
Then, the net force in the direction of the rope is equal to:

By the second law of Newton, this force is equal to mass times acceleration, so we can solve for acceleration as follows:

So, the first person accelerates at 4.38 m/s².

Now, we need to find the length of the rope. Using the Pythagorean theorem, we get:

`\begin{gathered} L=\sqrt[]{60^2+30^2} \\ L=\sqrt[]{3600+900} \\ L=\sqrt[]{4500}=67.08\text{ m} \end{gathered}`

Then, using a kinetic equation, we get:

`\begin{gathered} x=v_it+(1)/(2)at^2 \\ x=(1)/(2)at^2 \\ 2x=at^2 \\ (2x)/(a)=t^2 \\ t=\sqrt[]{(2x)/(a)} \end{gathered}`

Where x is the distance traveled, vi is the initial velocity, which is 0 m/s, a is the acceleration and t is the time.

Now, we can replace x by the length of the rope 67.08m and a by 4.38 to get:

`t=\sqrt[]{(2(67.08))/(4.38)}=5.54\text{ s}`

So, the first person takes 5.54 s to reach the end of the zipline.

Therefore, the answers are

Acceleration = 4.38 m/s²

Time = 5.54 s