Given:
Distance the stone hits the stream = 32.5m below the released point
Time = 3.10 seconds
Let's find the speed of the stone just after it leaves your hand.
To find the speed of the stone, apply the kinematic formula:
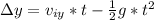
Since the point the stone hits the stream is below the released point is, the change in distance is:

Where:
a = -g = -9.8 m/s^2
t = 3.10 s
Substituet values into the formula and solve for the speed of the stone (vy).
We have:
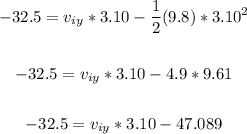
Solving further:
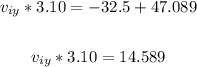
Divide both sides by 3.10:
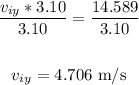
Therefore, the speed of the stone just after it leaves your hand is 4.706 m/s
ANSWER:
4.706 m/s