Question

In triangle ABC, angle C is a right angle. If cos A = 58, what is the value of cos B?

Answer 1

Question:

Solution:

The diagram of a triangle ABC, where C is the right angle is:

Now, by definition and according to the data of the problem, we get that:

`\cos (A)=(5)/(8)=\frac{adjacent\text{ side to the angle A}}{hypotenuse}`

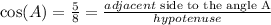
that is:

now, to find the cos(B), first, we must find the missing side of the triangle. To do that, we can apply the Pythagorean theorem:

`BC\text{ =}\sqrt[]{8^2-5^2}\text{ = }\sqrt[]{39}`

now, with respect to angle B, we obtain that:

`\cos (B)=\frac{adjacent\text{ side to the angle B}}{hypotenuse}=\frac{\sqrt[]{39}}{8}`

So that, we can conclude that the correct answer is:

`\frac{\sqrt[]{39}}{8}`