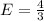Since the elongation E varies directly with the weight W, they are related as follows
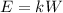
where k is the constant of proportionality. In order to find k, we can substitute the given values, that is, when E=2, W=15, then we have
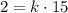
Then, k is given as
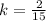
Therefore, our formula for any E and W is
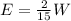
Now, in order to find E in the second case, by replacing W=10, we get
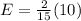
which yields
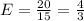
Therefore, the answer is