Question

Joshua is going to invest $9,000 and leave it in an account for 5 years. Assuming theinterest is compounded continuously, what interest rate, to the nearest tenth of apercent, would be required in order for Joshua to end up with $12,500?

Answer 1

Let r be the percent annual interest rate of the account. Since $9000 are left for 5 years, for an outcome of $12,500, then:

`9000*(1+(r)/(100))^5=12,500`

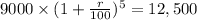
Divide both sides by 9000:

`(1+(r)/(100))^5=(12500)/(9000)=(25)/(18)`

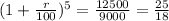
Take the 5th root to both sides:

`\begin{gathered} 1+(r)/(100)=\sqrt[5]{(25)/(18)} \\ \Rightarrow(r)/(100)=\sqrt[5]{(25)/(18)}-1 \\ \Rightarrow r=100(\sqrt[5]{(25)/(18)}-1) \end{gathered}`

Use a calculator to find the decimal expression for r:

`r=6.790716585\ldots`

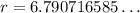
Therefore, to the nearest tenth:

`r=6.8`

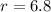
This means that Joshua would need to invest his money on a 6.8% annual interest account.