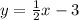consider two points closest to the line. say ,
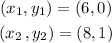
let us find the slope, m by the formula
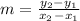
subsitute the points in the formula,
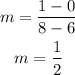
let us find the y - intercept.
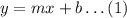
subsitute the one of the point (6,0) in the above equation.
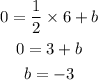
thus,
subsitute m= 1/2 and b = - 3 in the equation (1),