The rule of the division of differentiation is
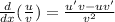
The given function is

a)
Let u the numerator and v the denominator
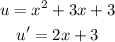
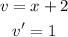
Substitute them in the rule above
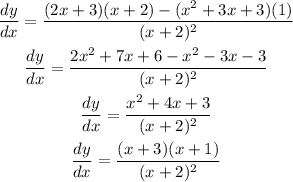
We will differentiate dy/dx again to find d^2y/dx^2
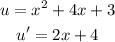
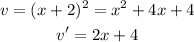
Then substitute them in the rule above
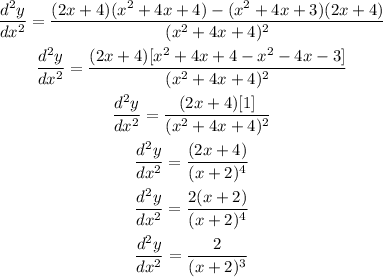
b)
The turning point is the point that has dy/dx = 0
Equate dy/dx by 0 to find the values of x
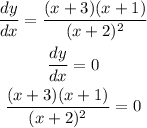
By using the cross multiplication
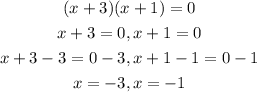
Substitute x by -3 and -1 in f(x) to find y

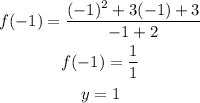
The turning points are (-3, -3) and (-1, 1)
c)
To find the inflection point equate d^2y/dx^2 by 0 to find x
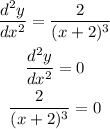
By using the cross multiplication
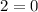
Which is wrong 2 can not be equal to zero, then
NO inflection point for the curve
d)
Since the denominator of the curve is x + 2, then
Equate it by 0 to find the vertical asymptote
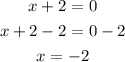
There is a vertical asymptote at x = -1
Since the greatest power of x up is 2 and the greatest power of down is 1, then there is an Oblique asymptote by dividing up and down
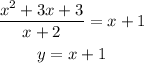
The Oblique asymptote is y = x + 1
No horizontal asymptote
e)
This is the graph of y = f(x)
This is the graph of y = f(IxI)
f)
For the curve
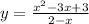
Take (-) sign as a common factor down, then
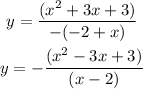
Since the sign of y is changed, then
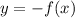
Then it is the reflection of f(x) about the y-axis we can see it from the attached graph
The red graph is f(x)
The purple graph is -f(x) which is the equation of the last part