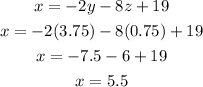Question

A county fair sells adult admission passes, child admission passes, and ride tickets. One family paid $29 for two adult passes,three child passes, and nine ride tickets. Another family paid $19 for one adult pass, two child passes, and eight ride tickets. A third family paid $51 for three adult passes,five child passes, and twenty one ride tickets. Find the individual costs of an adult pass,a child pass, and a ride ticket? Show all work

Answer 1

x= adult passes

y= child passes

z=ride tickets

the first family:

`2x+3y+9z=29\text{ (1)}`

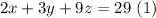
the sencond family

`x+2y+8z=19\text{ (2)}`

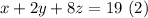
third family

`3x+5y+21z=51\text{ (3)}`

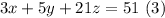
now we have the 3 equations, and we can solve x, y and z

for the equation of the second family we have:

`x=-2y-8z+19\text{ (4)}`

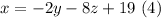
reeplace the new equation(4) in (1), we have:

`2(-2y-8z+19)+3y+9z=29`
`-4y-16z+38+3y+9z=29`
`y+7z=9\text{ (5)}`

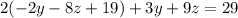
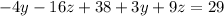
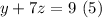
reeplace (4) in (3)

`3(-2y-8z+19)+5y+21z=51`
`-6y-24z+57+5y+21z=51`
`-y-3z=-6`
`y+3z=6\text{ (6)}`

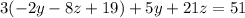
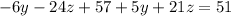
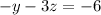
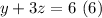
with 5 and 6, we have a 2x2 equation

that we can solve easier

solving 5 and 6, we have:

`\begin{gathered} y+7z=9 \\ y=9-7z\text{ (7)} \end{gathered}`

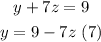
reeplace 7 in 6

`\begin{gathered} 9-7z+3z=6 \\ 4z=3 \\ z=(3)/(4)=0.75 \end{gathered}`

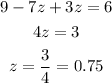
now we find y, reeplace z in (7)

`\begin{gathered} y=9-7(0.75) \\ y=9-5.25 \\ y=3.75 \end{gathered}`

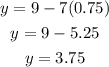
and finally we can find x, reeplacing y and z in (4)

`\begin{gathered} x=-2y-8z+19 \\ x=-2(3.75)-8(0.75)+19 \\ x=-7.5-6+19 \\ x=5.5 \end{gathered}`