Question

The fox population in a certain region has an annual growth rate of 9% per year. In the year 2012 there were 23,900 fox counted in the area. What is the fox population predicted to be in year 2020?What calculations and thinking did you use to find the answer?

Answer 1

Given:

The initial population is P(i) = 23,900.

The annual growth rate is r = 9% = 0.09.

The number of year is t = 2020-2012 = 8 years.

The objective is to find the population in the year 2020.

Step-by-step explanation:

The growth formula to find the final population is,

`P=P(i)*(1+r)^t\ldots\text{ . . . (1)}`

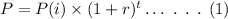
On plugging the given values in equation (1),

`P=23900(1+0.09)^8`

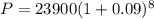
On further solving the above equation,

`\begin{gathered} P=23900(1.09)^8 \\ =47622.2471\ldots\text{.} \\ \approx47622 \end{gathered}`

Hence, the final population using the exponential growth formula is 47622.