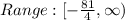Question

Instructions: For the following quadratic functions, write the function in factored form and then find the -intercepts, axis of symmetry, vertex, and domain and range. Round to one decimal place, if necessary.

Answer 1

Factored form: y = (x+1)(x-8)

x-intercept: (-1, 0) and (8, 0)

Axis of symmetry: x = 7/2

Vertex: (7/2, -81/4)

Domain: All real numbers

Range: y ≥ -81/4

Explanations:

Given the quadratic equation expressed as:

`y=x^2-7x-8`

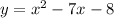
Factorize

`\begin{gathered} y=x^2-8x+x-8 \\ y=x(x-8)+1(x-8) \\ y=(x+1)(x-8)\text{ Factored form} \end{gathered}`

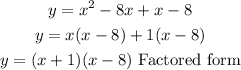
The x-intercept is the point where y= 0. Substitute y = 0 into the factored form

`\begin{gathered} (x+1)(x-8)=0 \\ x=-1\text{ }and\text{ }8 \\ The\text{ x-intercept are \lparen-1, 0\rparen and \lparen8, 0\rparen} \end{gathered}`

The axis of symmetry of the equation is given as x = -b/2a where:

a = 1

b = -7

Substitute:

`\begin{gathered} axis\text{ of symmetry:}x=(-(-7))/(2(1)) \\ axis\text{ of symmetry: }x=(7)/(2) \end{gathered}`

The vertex form of the equation is in the form (x-h)^2+k where (h, k) is the vertex. Rewrite in vertex form:

`\begin{gathered} y=x^2-7x-8 \\ y=x^2-7x+(-(7)/(2))^2-(-(7)/(2))^2-8 \\ y=(x-(7)/(2))^2-(49)/(4)-8 \\ y=(x-(7)/(2))^2-(81)/(4) \end{gathered}`

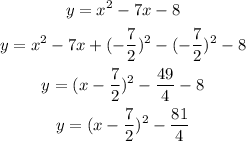
The vertex of the function will be (7/2, -81/4)

The domain are the independent values of the function for which it exists. The domain of the given quadratic function exists on all real number that is:

`Domain:(-\infty,\infty)`

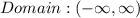
The range of the function are the dependent value for which it exist. For the given function, the range is given as:

`Range:[-(81)/(4),\infty)`