Question

Find the lengths of the missing sides in the triangle. Write your answers as integers or as decimals rounded to the nearest tenth. Not drawn to scale x= 6.9, y = 5.7 x=8, y = 11.3 x 11.3, y = 8 x = 5.7, y = 6.9

Answer 1

x=11.3 y=8

Step-by-step explanation

here we have a right triangle, so we can use a trigonometric function to find the missing sides

so

Step 1

a)let

`\begin{gathered} angle=45\text{ \degree} \\ opposite\text{ side=8} \\ adjacent\text{ side=y} \\ hypotenuse=x \end{gathered}`

Step 2

now, fin the missing length

a) y

to find the adjacent side we can use the stan function

`tan\theta=\frac{opposite\text{ side}}{adjacent\text{ side}}`

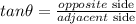
replace and solve for y( adjacent side)

`\begin{gathered} tan45=(8)/(y) \\ y=\frac{8}{tan\text{ 45}}=(8)/(1) \\ y=8 \end{gathered}`

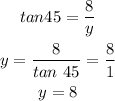
b)x (hypotenuse)

to find the hyoptenuse we can use the sin function ,

`\sin\theta=\frac{opposite\text{ side}}{hypotenuse}`

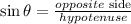
replace and solve for x

`\begin{gathered} sin\text{ 45=}(8)/(x) \\ x=\frac{8}{sin\text{ 45}}=11.3 \\ x=11.3 \end{gathered}`

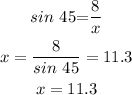
therefore, the answer is

x=11.3 y=8

I hope this helps you