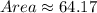Question

Calculate the area of the region enclosed by the x-axis and the curve y(x)=−x^2−3x+4.(show a figure and detailed answer please)

Answer 1

Given that the region is enclosed by the x-axis and this curve:

`y=-x^2-3x+4`

You can graph the function using a Graphic Tool:

Noice that the area region you must calculate is:

Notice that it goes from:

`x=-4`

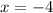
To:

`x=1`

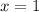
Therefore, you can set up that:

`Area=\int_(-4)^1(x^2-3x+4)-(0)dx`

In order to solve the Definite Integral, you need to:

- Apply these Integration Rules:

`\int x^ndx=(x^(n+1))/(n+1)+C`
`\int kf(x)dx=k\int f(x)dx`

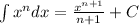
Then, you get:

`=((x^3)/(3)-(3x^2)/(2)+4)|^1_(-4)`

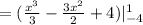
- Evaluate:

`=((1^3)/(3)-(3(1)^2)/(2)+4)-(((-4)^3)/(3)-(3(-4)^2)/(2)+4)`
`Area\approx64.17`

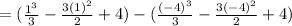
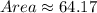
Hence, the answer is:

`Area\approx64.17`