Question

you have entered a 134-mile biathlon that consists of a run and a bicycle race. During your run, your average velocity is 6 miles per hour, and during your bicycle ace, your average velocity is 29 miles per hour. You finish the race in 7 hours. What is the distance of the run? What is the distance of the bicycle race?upposeWhat is the distance of the run?miles

Answer 1

Distance of the run: 18 miles

Distance of the bicycle race: 116 miles

Explanation:

Given:

Total distance = 134 miles

Total time = 7 hours

Average velocity during running = 6 mph

Average velocity during bicycle = 29 mph

Let x be the running distance and y be the bicycle distance.

We know that velocity equals distance in a given time, like this:

`\begin{gathered} v=(d)/(t) \\ \\ \text{ Therefore:} \\ \\ t=(d)/(v) \end{gathered}`

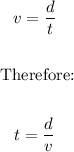
Knowing the above, we can establish the following system of equations:

`\begin{gathered} t_1+t_2=7\rightarrow(d_1)/(v_1)+(d_2)/(v_2)=7\rightarrow(x)/(6)+(y)/(29)=7\text{ \lparen1\rparen} \\ \\ x+y=134\rightarrow x=134-y\text{ \lparen2\rparen} \end{gathered}`

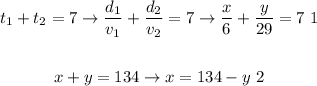
We substitute the second equation in the first and obtain the following:

`\begin{gathered} (134-y)/(6)+(y)/(29)=7 \\ \\ ((134-y)(29)+6y)/(6\cdot29)=7 \\ \\ (3886-29y+6y)/(174)=7 \\ \\ 3886-23y=7\cdot174 \\ \\ y=(1218-3886)/(-23)=(-2668)/(-23) \\ \\ y=116\rightarrow\text{ bicycle distance} \\ \\ \text{ now, for x:} \\ \\ x=134-116 \\ \\ x=18\rightarrow\text{ running distance} \end{gathered}`

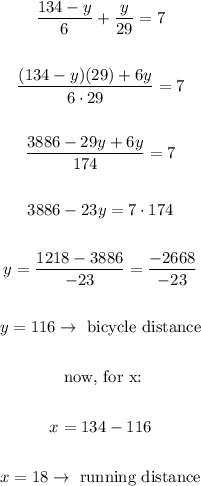
Therefore:

The distance of running is 18 miles and the distance by bicycle is 116 miles.