Question

In ACDE, mZC = (4x – 16), m D = (6x - 1)", and mZE = (4x - 13). Find mZC.

Answer 1

Step-by-step explanation:

We can do a diagram of triangle CDE:

The sum of the measures of the interior angles of any triangle is 180º. We can write an equation:

`\begin{gathered} m\angle C+m\angle D+m\angle E=180º \\ (4x-16)+(6x-1)+(4x-13)=180 \\ (4x+6x+4x)+(-16-1-13)=180 \\ 14x-30=180 \end{gathered}`

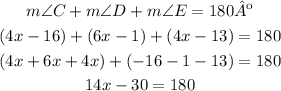
Solve for x:

`\begin{gathered} 14x=180+30 \\ 14x=210 \\ x=(210)/(14) \\ x=15 \end{gathered}`

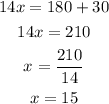
And with x = 15, replace into the expression for the measure of angle C to find it:

`m\angle C=4x-16=4\cdot15-16=60-16=44º`

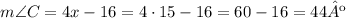
Answer:

m