Given the following quadratic expression:
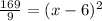
Let's check if the given equation can be solved by factoring.
a.) Let's determine the original equation.
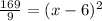
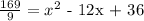

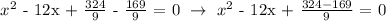

From the original equation, we observed that the constant 155/9 is not a perfect square. For the original quadratic equation to be factorable, we must apply the method of completing the square.
Therefore, we can say that the original quadratic equation can't be solved by factoring.