Step-by-step explanation
With the help of the given formula, we can find the first four terms of the sequence:
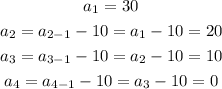
Then, the first four terms of the sequence are 30, 20, 10, 0, ...
Now, as we can see, this is an arithmetic sequence because there is a common difference between each term. The explicit formula of an arithmetic sequence is shown below:
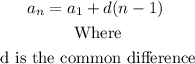
Then, we have:
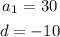

Thus, a formula for the general term of the sequence is:
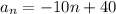
Now, we substitute n = 20 in the above formula to find the 20th term of the sequence:
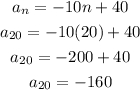
Answer
A formula for the general term of the sequence is:
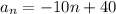
The 20th term of the sequence is -160.