Question

The ends of a triangular prism are right triangles with a base of 12 inches and height of 9 inches. The height of the prism is 11 inches what is the surface area?

Answer 1

Given:

The bases of triangular prism are right triangles with a base of 12 inches and height of 9 inches.

The height of the prism is 11 inches.

To find:

The surface area of the triangular prism.

Solution:

Using the Pythagoras theorem, the hypotenuse of the bases of the triangular prism is:

`Hypotenuse^2=Base^2+Height^2`

`Hypotenuse^2=12^2+9^2`

`Hypotenuse^2=144+81`

`Hypotenuse^2=225`

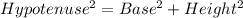
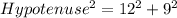
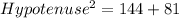
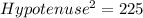
Taking square root on both sides.

`Hypotenuse=15`

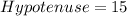
The surface after of the triangular prism contains 3 rectangles of dimensions 12 inches by 11 inches, 9 inches by 11 inches, 15 inches by 11 inches and two triangles with base 12 inches and height 9 inches.

Area of the rectangle:

`Area=Length * Width`

So, the area of three rectangles are:

`A_1=12 * 11`

`A_1=132`

`A_2=9 * 11`

`A_2=99`

`A_3=15 * 11`

`A_3=165`

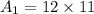
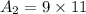
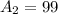
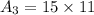
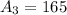
Area of a triangle is:

`Area=(1)/(2)* base * height`

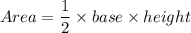
So, the area of the triangles is:

`A_4=(1)/(2)* 12 * 9`

`A_4=6 * 9`

`A_4=54`

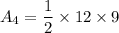
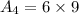
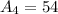
And, the triangles have same dimensions so their areas are equal.

`A_4=A_5=54`

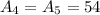
Now,

`Area=A_1+A_2+A_3+A_4+A_5`

`Area=132+99+165+54+54`

`Area=504`

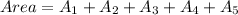
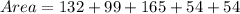
Therefore, the surface area of the triangular prism is 504 sq. inches.