Question

How much do I need to increase a radius of a circle to increase it's area 10 times?

Answer 1

Given that

It is said that we have to find the amount by which the radius will be increased such that the area is increased by 10 times.

Explanation -

The formula for the area of the circle is given as

`\begin{gathered} Area=\pi* r^2 \\ \\ A=\pi r^2-----------(i) \\ \\ where\text{ r is the radius of the circle.} \end{gathered}`

Now the new area is 10 times the previous one.

Let the new area be A' and the new radius be R.

Then,

`\begin{gathered} A^(\prime)=\pi* R^2 \\ \\ As\text{ A'=10}* A \\ \\ Then\text{ substituting the value of A' we have} \\ \\ 10* A=\pi* R^2 \end{gathered}`

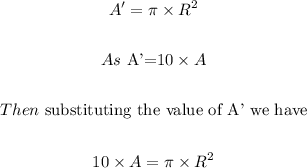
Now again substituting the value of A we have

`\begin{gathered} \pi* R^2=10*\pi* r^2 \\ \\ R^2=10r^2 \\ \\ R=√(10)* r \end{gathered}`

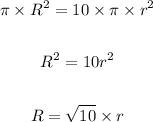
Hence the new radius will be √10 times the initial radius such that the area gets increased by 10 times.

Final answer - Therefore the final answer is √10 times.