You need to determine the number of possible combinations when you choose 4 appetizers out of 11 options in the dinner menu. Assuming that you are not going to repeat appetizers, to determine this number you have to apply combinations, using the formula:
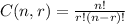
Where
n is the number of options available
r is the number of options you have to choose, with no repetition, and the order doesn't matter.
For this exercise:
n=11
r=4
The combination can be determined as follows:
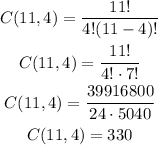
There are 330 combinations possible to choose 4 out of 11 appetizers from the menu.