Question

the graph shows that school's profit P for selling x lunches on one day.The school wants to change the price for lunch so that when it sells more than 30 lunches in one day, it begins to make a profit.How much would the school need to charge for each lunch situation?

Answer 1

Find the slope of the line. That will give us the present price for each lunch.

Use the points (0,-150) and (50,0):

`\begin{gathered} m=(0--150)/(50-0) \\ \Rightarrow m=3 \end{gathered}`

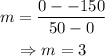
Then, the current profit equation is given by:

`y=3x-150`

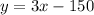
We want to change the price of each lunch so that the point (30,0) belongs to the graph (that means that when selling 30 lunches, it begins to make profit).

Let M be the new price. Then:

`\begin{gathered} 0=30M-150 \\ \Rightarrow30M=150 \\ \Rightarrow M=(150)/(30) \\ \therefore M=5 \end{gathered}`

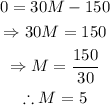
Therefore, the school should charge 5 dollars for each lunch.