To solve the exercise, first we are going to find the slope of the function f(x). Since we have a graph of the function, we can see two points through which the line passes:
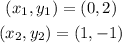
Now we can use this formula to find the slope:

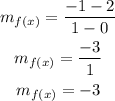
Then, the slope of the function f(x) is -3.
On the other hand, the function g(x) also describes a line and is written in slope-intercept form, that is:

Then, you can see that the slope of the function g(x) is -3, because
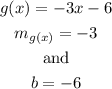
Therefore, the slope of f(x) is the same as the slope of g(x) and the correct answer is option A.