We have the sequence: 2, 6, 18, 54...
If the sequence is arithmetic, there must be a common difference between the terms that remains constant.
This is not the case for this sequence.
We can try by seeing if there is a common factor k such that:
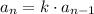
We can do it by:
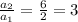
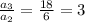
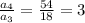
There, we have a geometric sequence, with factor k=3:
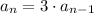
We can relate it to the first term as:
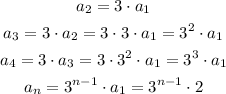
For n=12, we have:
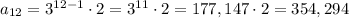
The value of a12 is 354,294.
The answer is d) Geometric, 354,294.