This system gives two equations
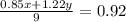
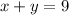
where x is the number pounds of $0.85/lb candy and y is the number of pounds of $1.22/lb candy.
The solution to the system is
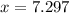
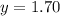
Hence, 7.297 lb of $0.85 candy is required in order that if we mix them with 1.70 lb of $1.22 candy, we will get a 9 lb solution of 0.92 /lb candy.