Question

solution of the system of equations.2. (3, 0) 2x+y=-63x + 2y = 94. (-2,3) y =2x+75x+y=-76. (0,-7) 2x -2y = 14X-Y=-7

Answer 1

We can solve these systems of equations as follows:

First Case

We have:

`\begin{cases}2x+y=-6 \\ 3x+2y=9\end{cases}`

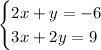
And we can solve this system by substitution as follows:

`\begin{gathered} 2x+y=-6 \\ 2x-2x+y=-6-2x \\ y=-6-2x \end{gathered}`

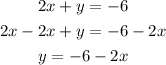
Now, we can substitute the corresponding value of y into the second equation as follows:

`\begin{gathered} y=-6-2x \\ 3x+2y=9 \\ 3x+2(-6-2x)=9 \\ 3x+(2)(-6)+(2)(-2x)=9 \\ 3x-12-4x=9 \\ 3x-4x-12=9 \\ -x-12=9 \\ -x-12+12=9+12 \\ -x=21\Rightarrow x=-21 \end{gathered}`

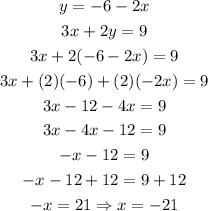
Now, we can substitute the value x = -21 into either of the original equations to find the value of y. We will use the first equation:

`\begin{gathered} 2x+y=-6 \\ 2(-21)+y=-6 \\ -42+y=-6 \\ -42+42+y=-6+42 \\ y=36 \end{gathered}`

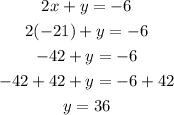
Therefore, the solution to this first system is (-21, 36).

We can check this result if we substitute both values into the original equations:

`\begin{gathered} \begin{cases}2x+y=-6 \\ 3x+2y=9\end{cases} \\ x=-21,y=36 \\ \begin{cases}2(-21)+36=-6 \\ 3(-21)+2(36)=9\end{cases} \\ \begin{cases}-42+36=-6 \\ -63+72=9\end{cases} \\ \begin{cases}-6=-6\Rightarrow This\text{ is true.} \\ 9=9\Rightarrow This\text{ is true.}\end{cases} \end{gathered}`

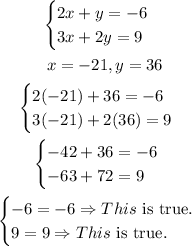
Therefore, the solution to the first system of equations is (-21, 36).

Second Case

`\begin{cases}y=2x+7 \\ 5x+y=-7\end{cases}`

We can rewrite the system as follows:

`\begin{cases}-2x+y=7 \\ 5x+y=-7\end{cases}`

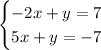
And we can solve this system by the elimination method: We have to multiply one of the equations by -1 and then add them algebraically as follows:

`\begin{gathered} \begin{cases}-2x+y=7 \\ -1(5x+y=-7)\end{cases} \\ \begin{cases}-2x+y=7 \\ (-1)(5x)+(-1)(y)=(-1)(-7)\end{cases} \\ \begin{cases}-2x+y=7 \\ -5x-y=7\end{cases} \end{gathered}`

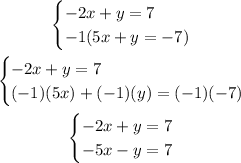
If we add both equations, then we have:

`\begin{gathered} \frac{\begin{cases}-2x+y=7 \\ -5x-y=7\end{cases}}{-7x=14} \\ -(7x)/(-7)=(14)/(-7) \\ x=-2 \end{gathered}`

And now we can substitute this value in either equation to find y:

`\begin{gathered} y=2x+7 \\ y=2(-2)+7 \\ y=-4+7 \\ y=3 \end{gathered}`

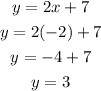
And we got y = 3.

Therefore, the solution to this system is equal to (-2, 3), and we can also check the solutions using the original equations:

`\begin{gathered} \begin{cases}y=2x+7 \\ 5x+y=-7\end{cases} \\ \begin{cases}3=2(-2)+7 \\ 5(-2)+3=-7\end{cases} \\ \begin{cases}3=-4+7 \\ -10+3=-7\end{cases} \\ \begin{cases}3=3\Rightarrow This\text{ is true.} \\ -7=-7\Rightarrow This\text{ is true.}\end{cases} \end{gathered}`

In summary, we have that:

The solution to the first system ---> (-21, 36).

The solution to the second system ---> (-2, 3).