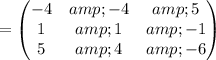Okay, here we have this:
We need to find the inverse of the matrix, let's do it:
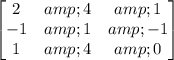
For that we are going to make the augmented form with the identity matrix and convert the original matrix into the identity:
![\begin{gathered} \begin{pmatrix}2 & 4 & 1 & | & 1 & 0 & 0 \\ -1 & 1 & -1 & | & 0 & 1 & 0 \\ 1 & 4 & 0 & | & 0 & 0 & 1\end{pmatrix} \\ =\begin{pmatrix}2 & 4 & 1 & | & 1 & 0 & 0 \\ 0 & 3 & -(1)/(2) & | & (1)/(2) & 1 & 0 \\ 1 & 4 & 0 & | & 0 & 0 & 1\end{pmatrix}\text{ }R_2\leftarrow R_2+(1)/(2)R_1 \\ =\begin{pmatrix}2 & 4 & 1 & | & 1 & 0 & 0 \\ 0 & 3 & -(1)/(2) & | & (1)/(2) & 1 & 0 \\ 0 & 2 & -(1)/(2) & | & -(1)/(2) & 0 & 1\end{pmatrix}\text{ }R_3\leftarrow R_3-(1)/(2)R_1 \\ =\begin{pmatrix}2 & 4 & 1 & | & 1 & 0 & 0 \\ 0 & 3 & -(1)/(2) & | & (1)/(2) & 1 & 0 \\ 0 & 0 & -(1)/(6) & | & -(5)/(6) & -(2)/(3) & 1\end{pmatrix}R_3\leftarrow R_3-2/3R_2 \\ =\begin{pmatrix}2 & 4 & 1 & | & 1 & 0 & 0 \\ 0 & 3 & -(1)/(2) & | & (1)/(2) & 1 & 0 \\ 0 & 0 & 1 & | & 5 & 4 & -6\end{pmatrix}R_3\leftarrow-6R_3 \\ =\begin{pmatrix}2 & 4 & 1 & | & 1 & 0 & 0 \\ 0 & 3 & 0 & | & 3 & 3 & -3 \\ 0 & 0 & 1 & | & 5 & 4 & -6\end{pmatrix}R_2\leftarrow R_2+(1)/(2)R_3 \\ =\begin{pmatrix}2 & 4 & 0 & | & -4 & -4 & 6 \\ 0 & 3 & 0 & | & 3 & 3 & -3 \\ 0 & 0 & 1 & | & 5 & 4 & -6\end{pmatrix}R_1\leftarrow R_1-R_3 \\ =\begin{pmatrix}2 & 4 & 0 & | & -4 & -4 & 6 \\ 0 & 1 & 0 & | & 1 & 1 & -1 \\ 0 & 0 & 1 & | & 5 & 4 & -6\end{pmatrix}R_2\leftarrow(1)/(3)R_2 \\ =\begin{pmatrix}2 & 0 & 0 & | & -8 & -8 & 10 \\ 0 & 1 & 0 & | & 1 & 1 & -1 \\ 0 & 0 & 1 & | & 5 & 4 & -6\end{pmatrix}R_1\leftarrow R_1-4R_2 \\ =\begin{pmatrix}1 & 0 & 0 & | & -4 & -4 & 5 \\ 0 & 1 & 0 & | & 1 & 1 & -1 \\ 0 & 0 & 1 & | & 5 & 4 & -6\end{pmatrix}R_1\leftarrow(1)/(2)R_1 \end{gathered}]()
Finally the inverse is on the right side of the augmented matrix: