We are given the point (-2,4) and the line y=2x+9. We want the equation of the line that passes through the given point and that is perpendicular to the given line.
To do so, we will use the following equation of a line
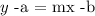
in this equation, m is the slope of the line and (a,b) is a point in the line. In our case, we are given that (-2,4) is in the line. That is, a=-2 and b=4. So our equation becomes
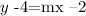
or equivalently

now, we only need to find the value of m. To do so, we use the given line and the fact that the product of the slopes of perpendicular lines is -1.
The given line (2x+9) has a slope of 2. So, we have the following equation
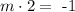
so if we divide both sides by 2, we get that
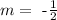
So the equation we are looking for becomes
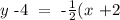
We want this equation in the slope intercept form. So we operate to find y in this equation. So first, we distribute on the right hand side. We get
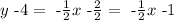
now we add 4 on both sides, so we get
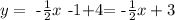
we can check that if x= -2 we get

which confirms that the point (-2,4) is on the line