Recall that :
1) A function
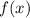
translated n-units to the left is
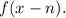
2) A function
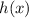
translated m-units up is:
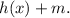
3) A function g(x) reflected over the x-axis is:
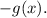
The parent function is:
![y=\sqrt[]{x}\text{.}](https://img.qammunity.org/2023/formulas/mathematics/college/yu7jbgmkyz2vr2holk9ip99bsc92ttg0g8.png)
The function of the graph of the above function translated horizontally 3 units to the left is:
![y=\sqrt[]{x+3}.](https://img.qammunity.org/2023/formulas/mathematics/college/xzqx6cvax4x5wsdhx7swnlfiep4tg6xj1g.png)
The function of the graph of the above function translated vertically 4 units up is:
![y=\sqrt[]{x+3}+4.](https://img.qammunity.org/2023/formulas/mathematics/college/pcyhwjnjmyq7b2g5e1erkeocq8jkwu6gif.png)
The function of the graph of the above function reflected over the x-axis is:
![y=-(\sqrt[]{x+3}+4)=-\sqrt[]{x+3}-4.](https://img.qammunity.org/2023/formulas/mathematics/college/iidvrp7czs1dom8eb2e4f56lq1h1norifv.png)
Finally, the function of the graph of the above function stretched vertically by a scale factor of 2 is:
![y=-2\sqrt[]{x+3}-4.](https://img.qammunity.org/2023/formulas/mathematics/college/quutp884kktd0hbo54xvnrqfds07cli6je.png)
Answer:
The graph of the function has a horizontal translation Left 3 and vertical translation Up 4. The graph has been reflected over the x-axis and has been Vertically stretched.