Question

(I need this as an actual equation and solution not just which one it is.. also any people just trying to get credits will result in a report.) The temperature of a cooling liquid is given by the function T(m) = 38 (0.82)" +21, where T represents the temperature in degrees Celsius and m represents the number of minutes, m≥0, that the liquid has been cooling. Which of the following represents a temperature that the liquid does not reach as it cools down?

(1) 53
(2) 16
(3) 41
(4) 28​

Answer 1

(2) 16°C

Explanation:

`T(m)=38(0.82)^m+21`

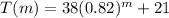
Find the temperature at the outset (
`m=0`):

`T(0)=38(0.82)^0+21`

`T(0)=38(1)+21`

`T(0)=38+21`

`T(0)=59`

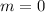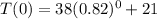
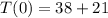
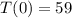
Since the liquid is cooling, all temperatures equal to or less than 59°C are valid possibilities. However, over time (represented as
`m\rightarrow\infty`),
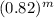`(0.82)^m` is reduced towards zero and, as such,
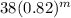`38(0.82)^m` will be reduced towards zero. All that will remain is
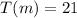`T(m)=21`, which makes it the horizontal asymptote. This is shown in the attached graph.

Therefore, since 16°C falls below the asymptote, it does not represent a temperature that the liquid reaches as it cools down.