Answer:
-20+48i
Step-by-step explanation:
The solution erroneously began by expressing the square as the square of each of the terms.
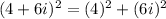
However, the correct way is to take the square of the entire expression inside the bracket as shown below:
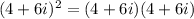
Next, we expand and simplify our result below:
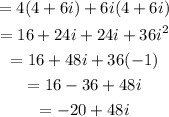
The result of the operation in standard form is -20+48i.