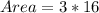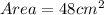Question

LMN is a right-angle triangle. Angle NLM=90. PQ is parallel to LM. The area of triangle PNQ is 8cm^2. The area of triangle LPQ is 16cm^2. Work out the area of triangle

Answer 1

The area of LQM is
`48cm^2`

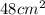
Explanation:

Given

Area of PNQ = 8

Area of LPQ = 16

See attachment for triangles

The area of PNQ is calculated as:

`Area = (1)/(2) * PQ * PN`

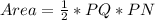
Substitute 8 for Area

`8 = (1)/(2) * PQ * PN`

`PQ * PN = 16`

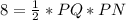
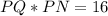
The area of LPQ is calculated as:

`Area = (1)/(2) * PQ * LP`

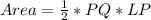
Substitute 16 for Area

`16= (1)/(2) * PQ * LP`

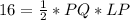
From the attachment:

`PN + LP =LN`

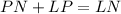
Make LP the subject

`LP = LN -PN`

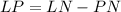
So:

`16= (1)/(2) * PQ * (LN -PN)`

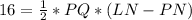
We have:

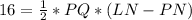`16= (1)/(2) * PQ * (LN -PN)` and
`PQ * PN = 16`

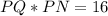
Equate both expressions:

`(1)/(2) * PQ *(LN - PN) = PQ * PN`

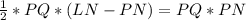
Divide both sides by PQ

`(1)/(2) (LN - PN) = PN`

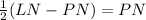
Multiply both sides by 2

`LN - PN = 2PN`

`LN= 3PN`

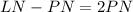
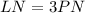
Since PNQ is similar to LNM, the following equivalent ratios exist:

`(LM)/(PQ) = (LN)/(PN)`

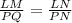
Substitute
`LN= 3PN`

`(LM)/(PQ) = (3PN)/(PN)`

`(LM)/(PQ) = 3`

`LM = 3PQ`

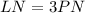
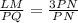
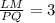
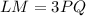
Area of LQM is:

`Area = (1)/(2) * LM * LP`

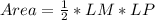
This gives:

`Area = (1)/(2) * 3PQ * LP`

`Area = 3 *(1)/(2) *PQ * LP`

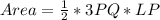
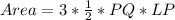
Recall that:

`16= (1)/(2) * PQ * LP`

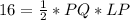
So:

`Area = 3 *16`

`Area = 48cm^2`