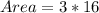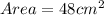Answer:
The area of LQM is
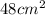
Explanation:
Given
Area of PNQ = 8
Area of LPQ = 16
See attachment for triangles
The area of PNQ is calculated as:
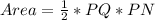
Substitute 8 for Area
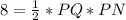

The area of LPQ is calculated as:

Substitute 16 for Area

From the attachment:
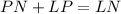
Make LP the subject
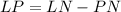
So:

We have:
 and
and

Equate both expressions:

Divide both sides by PQ
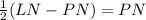
Multiply both sides by 2
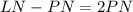
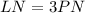
Since PNQ is similar to LNM, the following equivalent ratios exist:
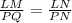
Substitute
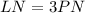
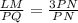
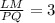
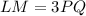
Area of LQM is:
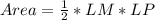
This gives:
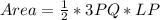
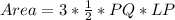
Recall that:

So: