Question

{57, 53, 53, 71, 73, 57, 61, 58, 78. 64, 54, 69, 56, 58, 49, 56, 53, 52, 82, 62, 61, 60, 71, 75, 60} Whats the mean?. and the iqr? what is the five number summary? what is Q3? The Median is 60.

Answer 1

Given the data set:

`\lbrace57,53,53,71,73,57,61,58,78,64,54,69,56,58,49,56,53,52,82,62,61,60,71,75,60\rbrace`

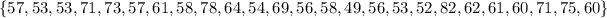
• You can find the Mean by adding all the values and dividing the sum by the number of values in the data set:

`Mean=(57+53+53+71+73+57+61+58+78+64+54+69+56+58+49+56+53+52+82+62+61+60+71+75+60)/(25)`
`Mean\approx61.72`

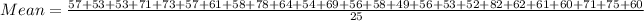
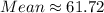
• By definition the term for the third quartile can be found with this formula:

`(3)/(4)(n+1)`

Where "n" is the number of observations.

In this case:

`n=25`

Then:

`(3)/(4)(25+1)\approx19.5`

Since it is an integer, you get that the position of the terms is:

`Q_3=(69+71)/(2)=70`

Because, when you order the data set, 69 is the 19th value and 71 is the 20th value. Then, the third quartile is the average between them:

`\lbrace49,52,53,53,53,54,56,56,57,57,58,58,60,60,61,61,62,64,69,71,71,73,75,78,82\rbrace`

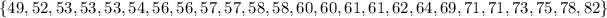
• By definition:

`IQR=Q_3-Q_1`

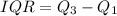
And the term position of the first quartile is found with:

`(n+1)/(4)`

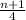
You get:

`(25+1)/(4)=6.5`

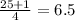
Therefore, you can determine that:

`Q_1=(54+56)/(2)=55`

Then:

`IQR=70-55=15`

• By definition, the Five-Number Summary is:

- The minimum value:

`Minimum=49`

- The first quartile:

`Q_1=55`

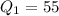
- The median:

`Median=60`

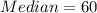
- The third quartile:

`Q_3=70`

- The maximum value:

`Maximum=82`

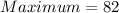
Hence, the answers are:

• Mean:

`Mean\approx61.72`

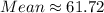
• IQR:

`IQR=15`

• Five-Number Summary:

`Minimum=49`
`Q_1=55`
`Median=60`

`Q_3=70`

`Maximum=82`

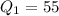
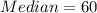
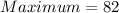
• Third quartile:

`Q_3=70`