Question

Hi can you help me find the correct answer to this?

Answer 1

x=3 , 8

Step-by-step explanation

remember the square of a binomyal

`(a\pm b)^2=a^2\pm2ab+b^2`

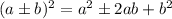
Step 1

given

`√(x+1)\text{ =x-5}`

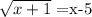
we need to isolate x, so

a) rise each side to power 2

`\begin{gathered} √(x+1)\text{ =x-5} \\ (√(x+1))\text{ }=(x-5)^2 \\ x+1=x^2-2*5*x+5^2 \\ x+1=x^2-10x+25 \\ subtrac\text{ x in both sides} \\ x+1-x=x^2-10x+25-x \\ 1=x^2-11x+25 \\ subtract\text{ 1 in both sides} \\ 1-1=x^2-11x+25-1 \\ hence \\ x^2-11x+24=0 \end{gathered}`

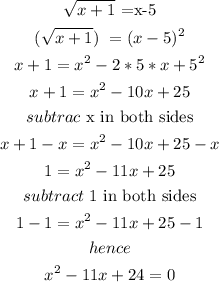
Step 2

solve the quadratic equation:

b) use the quadratic formula

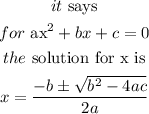
`\begin{gathered} it\text{ says} \\ for\text{ ax}^2+bx+c=0 \\ the\text{ solution for x is} \\ x=(-b\pm√(b^2-4ac))/(2a) \end{gathered}`

so

i)let

`\begin{gathered} ax^2+bx+c=x^2-11x+24 \\ so \\ a=1 \\ b=-11 \\ c=24 \end{gathered}`

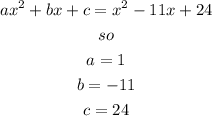
ii) now, replace in the formula

`\begin{gathered} x=(-b\pm√(b^2-4ac))/(2a) \\ x=(-(-11)\pm√(-11^2-4(1)(24)))/(2(1)) \\ x=(11\pm√(121-96))/(2) \\ x=(11\pm√(25))/(2)=(11\pm5)/(2) \\ so \\ x_1=(11+5)/(2)=(16)/(2)=8 \\ x_2=(11-5)/(2)=(6)/(2)=3 \end{gathered}`

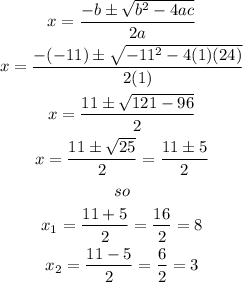
therefore, the solutions are x= 3 and x= 8

so, the answer is

x=3 , 8

I hope this helps you