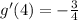Given that:
![g(x)=\sqrt[]{x}f(x)](https://img.qammunity.org/2023/formulas/mathematics/college/2azvol96wtj7nyat2hux597zcni0869ktt.png)
You need to find:
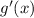
In order to derivate the function, you need to apply the Product Rule
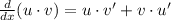
Then, you get:
![g^(\prime)(x)=\sqrt[]{x}\cdot f^(\prime)(x)+f(x)(\sqrt[]{x})^(\prime)](https://img.qammunity.org/2023/formulas/mathematics/college/z1l6b2lweggct3yss4lyrr8u7s3gls1blg.png)
Since:
![\sqrt[]{x}=x^{(1)/(2)}](https://img.qammunity.org/2023/formulas/mathematics/college/qs7vpqo09ne5jtgklc0yiwbw2nxtgclx0u.png)
You know that:
![(d)/(dx)(\sqrt[]{x})=(1)/(2)x^{(1)/(2)-1}=(1)/(2)x^{-(1)/(2)}=\frac{1}{2\sqrt[]{x}}](https://img.qammunity.org/2023/formulas/mathematics/college/lrl9050zt8v8wzdeu7mlkeubwwmkbw16qy.png)
Hence:
![\begin{gathered} g^(\prime)(x)=\sqrt[]{x}\cdot f^(\prime)(x)+f(x)(\frac{1}{2\sqrt[]{x}}) \\ \\ g^(\prime)(x)=\sqrt[]{x}\cdot f^(\prime)(x)+\frac{1}{2\sqrt[]{x}}f(x) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/susxsyzedeup2ifvk9y5zx5sid0q4s3lgp.png)
Knowing that you need to find:
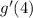
You can rewrite the function as follows:
![g^(\prime)(4)=\sqrt[]{4}\cdot f^(\prime)(4)+\frac{1}{2\sqrt[]{4}}f(4)](https://img.qammunity.org/2023/formulas/mathematics/college/i4rh9ov5v79j9e0y28ex2e0pybql9qodb2.png)
Knowing that:
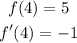
You can substitute values:
![g^(\prime)(4)=(\sqrt[]{4})(-1)+(\frac{1}{2\sqrt[]{4}})(5)](https://img.qammunity.org/2023/formulas/mathematics/college/1hnaechwscinaonms6m6zct10w4idh1bj4.png)
Evaluating, you get:
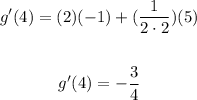
Hence, the answer is: