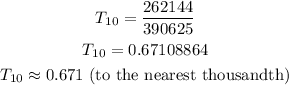Question

Arithmetic and Geometric Sequences. The first three terms of a sequence are given. Round to the nearest thousandth (if necessary).

Answer 1

From the information provided, observe that the three terms are connected by a common ratio.

The first term is multiplied by a value denoted as letter r (common ratio) to derive the second term. The second term is also multiplied by r to derive the third term, and so on.

Therefore;

`\begin{gathered} 5* r=4 \\ r=(4)/(5) \\ 4* r=(16)/(5) \\ r=(16)/(5)\text{ / }(4)/(1) \\ r=(16)/(5)*(1)/(4) \\ r=(4)/(5) \end{gathered}`

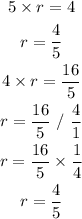
From the above calculation, the common ratio is 4/5. Therefore, the 10th term in the sequence shall be;

`\begin{gathered} T_n=a* r^(n-1) \\ \text{Where;} \\ a=5,r=(4)/(5),n=\text{nth term} \\ T_(10)=5*((4)/(5))^(10-1) \\ T_(10)=5*((4)/(5))^9 \\ T_(10)=5*(262144)/(1953125) \\ T_(10)=(262144)/(390625) \end{gathered}`

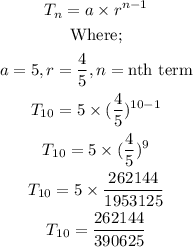
The 10th term is as shown above. To round this figure to the nearest thousandth, we need to convert this fraction into a decimal.

Hence we would have;

`\begin{gathered} T_(10)=(262144)/(390625) \\ T_(10)=0.67108864 \\ T_(10)\approx0.671\text{ (to the nearest thousandth)} \end{gathered}`