Question

A city has a population of 300,000 people. Suppose that each year the population grows by 4.5%. What will the population be after 14 years?Use the calculator provided and round your answer to the nearest whole number.

Answer 1

Given:

Population =300000

Growth rate = 4.5 %.

time = 14 years.

consider the exponential growth equation.

`y=a(1+r)^t`

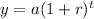
where a is the initial value and r=growth rate.

Let y be the number of population after t years.

Substitute a=300000, r=4.5/100. t-14 in exponential growth equation, we get

`y=300000(1+(4.5)/(100))^(14)`

`y=300000((100)/(100)+(4.5)/(100))^(14)`

`y=300000((104.5)/(100))^(14)`

`y=300000(1.045)^(14)`
`y=555583.476485`

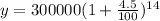
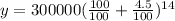
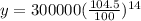
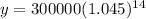
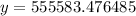
Hence the population after 14 years is 555584 people.