Question

ProbabilityHello need help Thank you. A phone number in Cameroon consists of 9 digits. From the theoretical capacity of the Cameroonian telephone network, say whether the 4 current operators (CAMTEL MTN, NEXTTEL and ORANGE) can meet a demand for 150 million subscriptions. 1) How many different ways can you arrange four people in four numbered chairs? 2)How many ways can you distribute 10 balloons to 3 children, 4 for the first and 3 for each of the other two?

Answer 1

1) 24

2)66

Step-by-step explanation:

1) How many different ways can you arrange four people in four numbered chairs?

Answer: we have 4 people ands 4 chairs, so we use the factorial of 4 to find the number of ways that we can arrenge the people:

`4!\text{ = 4}\cdot3\cdot2\cdot1=24`

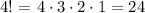
we can arrange 4 people in 4 chairs in 24 different ways

2)How many ways can you distribute 10 balloons to 3 children?

To distribute "n" objects to "r" people (in this case n=10, and r = 3) we use the following combinarions formula:

`C(n+r-1,r-1)`

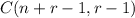
substituting our values we get:

`C(10+3-1,3-1)`
`C(12,2)`

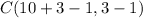
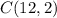
and since C(a,b) is defined as:

`C(a,b)=(a!)/(b!(a-b)!)`

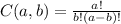
For C(12,2) we get the following:

`C(12,2)=(12!)/(2!(12-2)!)`

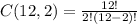
which simplifies to:

`C(12,2)=(12!)/(2!(10)!)=66`

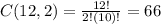
We can distribute 10 balloons to 3 people in 66 ways