Question

14. The measure of one side of an equilateral triangle is (s+6) inches long. Write 2 different, equivalent

expressions to represent the perimeter of the triangle.

Answer 1

Answer:

Perimeter of the equilateral triangle = 3(s + 6) inches

Perimeter of the equilateral triangle = 3s + 18 inches

Step-by-step explanation:

Given:

One of the sides of an equilateral triangle = (s + 6)

To find:

2 different equivalent expressions that represent the perimeter of the triangle

To determine the expression, we need to apply the formula for the perimeter of an equilateral triangle

`\begin{gathered} Perimeter\text{ of equilateral triangle = sum of all 3 sides} \\ since\text{ all sides of an equilateral triangle are equal,} \\ Perimeter\text{ = 3}*\text{ one of the side} \end{gathered}`
`\begin{gathered} one\text{ of the side = s + 6} \\ \\ Perimter\text{ = 3 }*(s\text{ + 6\rparen} \\ Perimeter\text{ of the equilateral triangle = 3\lparen s + 6\rparen inches} \end{gathered}`

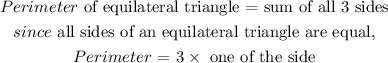
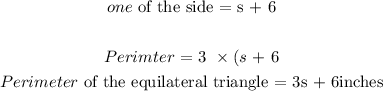
Another expression for the perimeter:

`\begin{gathered} Perimeter\text{ = 3\lparen s + 6\rparen} \\ Expanding\text{ the parenthesis using distributive property:} \\ Perimeter\text{ = 3\lparen s\rparen + 3\lparen6\rparen} \\ Perimeter\text{ of the equilateral triangle = 3s + 18 inches} \end{gathered}`