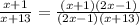The given fractions are,
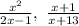
The LCD of fractions is the least common multiple of the denominators.
So, the LCD of the above fractions is,

Multiplying the numerator and the denominator of the fraction by a common term does not change the fraction.
So, the first fraction can be expressed in terms of the LCD as,

The second fraction can be expressed in terms of the LCD as,