Answer:
• (a)112 feet
,
• (b)1.28125 seconds.
,
• (c)138.265625 feet.
,
• (d)4.22091 seconds
Explanation:
The height of the rocket in terms of the number of seconds t since the rocket's engine stops firing is given below.
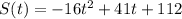
Part A
At the time the rocket stopped firing, t=0.
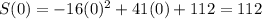
The rocket was 112 feet above the ground when it stopped firing.
Part B
The value of t at which the rocket reaches its maximum height is the equation of the line of symmetry.
To find this equation, we use the formula below.
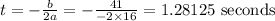
The rocket reaches its maximum height after 1.28125 seconds.
Part C
To find the maximum height, substitute t=1.28125 into S(t).
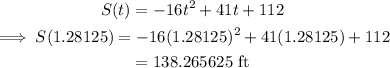
The maximum height of the rocket is 138.265625 feet.
Part D
When the rocket hits the ground, the height is 0.
Set S(t)=0 and solve for t as follows.
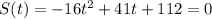
Using the quadratic formula:
![\begin{gathered} t=\frac{-41\pm\sqrt[]{41^2-4(-16)(112)}}{2*-16}=\frac{-41\pm\sqrt[]{1681-(-7168)}}{-32} \\ =\frac{-41\pm\sqrt[]{1681+7168}}{-32} \\ =\frac{-41\pm\sqrt[]{8849}}{-32} \\ t=\frac{-41+\sqrt[]{8849}}{-32}\text{ or }t=\frac{-41-\sqrt[]{8849}}{-32} \\ t=-1.658\; \text{or }t=4.22091 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/pmbquu8knrw0ns3m5izykxuoanppm3wr8l.png)
Since t cannot be negative, the rocket will hit the ground after 4.22091 seconds.