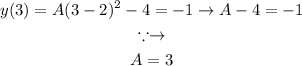Question

The vertex of this parabola Is at parabola is at (2,-4)

Answer 1

`A=3`

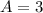
Step-by-step explanation: We are given two points, P1 is vertex and P2 is another point on the parabola:

`\begin{gathered} P_1(2,-4) \\ P_2(3,-1) \end{gathered}`

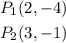
The general form of the equation of a parabola is:

`y(x)=A(x\pm B)^2+C`

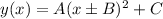
Where A is the Coefficient of the parabola function which is responsible for compression and stretch, likewise B is responsible for the translation along the x-axis and C is responsible for translation along the y-axis.

We know that our function is translated 2 units towards the right and 4 units downwards:

Therefore:

`\begin{gathered} B=-2 \\ C=-4 \end{gathered}`

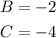
And this turns the parabola equation into:

`y(x)=A(x-2)^2-4`

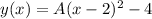
Using P2 we can find the constant-coefficient as:

`\begin{gathered} y(x)=A(x-2)^2-4_{} \\ P_2(3,-1) \\ \\ \\ \end{gathered}`

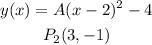
Therefore:

`\begin{gathered} y(3)=A(3-2)^2-4=-1\rightarrow A-4=-1 \\ \because\rightarrow \\ A=3 \end{gathered}`