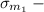Given:
The standard deviation are given as,
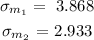
Required:
The standard deviation of the sample mean differences.
Step-by-step explanation:
The formula for the deviation of the sample mean difference is given as,
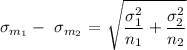
Substituting the values in the above formula,
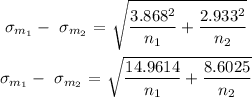
Answer:
Thus the required answer is,