Given: The function below
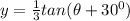
To Determine: The amplitude, the period, and the phase shift
Solution
The graph of the function is as shown below
The general equation of a tangent function is
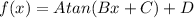
Where

Let us compare the general form to the given
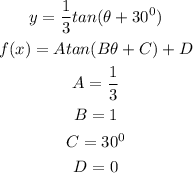
Therefore
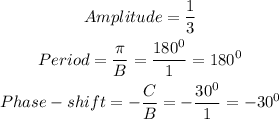
Hence, the correct option is as shown below